|
7. Harmonious Sound Waves
All music, based upon melody and rhythm
is the earthly representative of heavenly music.
Plotinus
When I first heard the singing bowls, I perceived a harmonious blend
of sounds. After a few weeks I began to distinguish the different tones
in each bowl. These are the partials, and a trained musician is able to
appreciate their richness immediately. Singing bowls are actually far
more complex and rich in partials than anyone can distinguish
completely. A computer with a microphone and a sound program helps us
look a little deeper into the intriguing world of sound waves, showing
how beautiful and complex the sound waves of the singing bowls really
are.
To fully comprehend the sound analysis of singing bowls, an
understanding of the acoustics of bells is needed. The ring of a bell,
or singing bowl, is always focused near the rim, where the maximum
elastic movement and resonance occur. To get the full potential of the
sound it is necessary to strike a bowl on its rim. Each bowl has unique
patterns of vibrations that produce a great number of sound frequencies.
Visualize a tuning fork as a thin vertical slice of a bowl, then imagine
the bowl as a set of tuning forks bound together. Although a singing
bowl has no stem, like a tuning fork there is a node (point of no
movement) near the base, with the wall of the bowl resonating like the
prongs of a tuning fork. Both tuning forks and singing bowls have other
intermediate nodal regions associated with higher frequencies, or
partials. In a tuning fork the intensity of the partials is purposely
subdued, while in a bowl or bell the series of frequencies along nodal
regions between the rim and the node at the base is enhanced.
Irregularities in the cutaway profile of a singing bowl are responsible
for the character of the vibrations, determining not only the
frequencies the partials but also their intensities. This explains the
wide range in sound quality, timbre, and partials among the hand-crafted
singing bowls. No two are alike.
One of the most obvious differences
when comparing singing bowls to each other is the duration of the sound.
Some have a long sustained ring, while others stop within a few seconds.
The duration of the ring is dependent upon material, size and profile.
The metal must be sufficiently hard. Hardness depends upon the
proportion of tin in relation to copper. More than one percent of lead
will weaken the alloy and have an adverse effect on the duration of the
tone. Larger masses of metal are capable of more acoustical energy and
will vibrate longer. Among my collection of singing bowls, the ones that
vibrate the longest with the strongest sound have considerably more mass
in relation to their size. The thick walls and rims produce strong,
clear sounds with harmonious partials.
When the rim of a singing bowl
is hit by a striker, the bowl’s wall is momentarily forced out of the
round into a more elliptic shape. The distortion sets the small
tuning-fork-like cross-sectional areas into vibration. In the region of
impact, they are forced outward, while one-quarter around the bowl’s
periphery from the point of strike the motion responds inwardly. The
alternating inward and outward movement produces the fundamental pitch
and the hum tone. The result is four nodal points on the circumference
which produce four equidistant vertical nodal lines, or meridians, from
the rim to the nodal point at the base of the bowl. Further nodal
meridians are formed because the bowl’s initial deformation is not a
pure ellipse. When a bowl is partially filled with water and struck, the
sound waves originating from these four meridians can clearly be seen
rippling over the surface. When you strike the bowl (with a padded
striker, you don’t want to break the bowl!) a little harder, the elastic
movement of the bowl’s wall will cause a fountain of water drops to
shoot up and out of the bowl.
What tones are generated when a bowl is
struck? Upon impact, the strike tone dominates momentarily. It wavers
and cannot be measured as a specific frequency. Below the fundamental is
the hum tone, vibrating the longest as it fades into infinity. The
partials of higher frequencies are of a shorter duration. In contrast to
singing bowls, bells are tuned to specific partials, mainly a minor
third, fifth, and octave. Because the acoustics of bells is complex,
tuning is essential to the harmonious blending of tones when two or more
bells are heard simultaneously. Because singing bowls are not tuned,
combinations of two bowls will not always sound right. However, some
will produce interesting and pleasing effects when played together.
With standard bells the frequencies of the first six or seven partials
adhere to a strict harmonious relationship to the fundamental. The upper
partials can be inharmonious because the vibrating segments of the bell,
where these upper partials are produced, are shorter. In sound analysis,
this is even more so with singing bowls. Only the first and second
partials have a near harmonious relationship to the fundamental. The
rest of the upper partials are inharmonious. Irregularities in the shape
of a bowl also contributes to this considerably.
After a singing bowl
has been struck tonal decay sets in as the energy is dissipated. The
partials fade at different rates. This shows up clearly in spectral
analysis. Higher frequencies dampen more rapidly than lower ones. Tonal
decay undergoes a subtle and continuing transformation which varies
according to the size and profile of the individual bowl. Spectral
analysis also shows the cyclic pulsation (periodic rising and falling in
intensity) of the partials. The intensity of some partials pulsates
strongly (a couple of times a second), while the others are almost
constant. Where does this flux come from? In a good bell perfect
symmetry produces an even ring. Occasionally the ring of a bell is
uneven, creating beats or pulsation. The causes of this are in the
casting: lack of symmetry, irregularities in thickness, and the
composition or homogeneity of the metal. This all occurs frequently with
singing bowls. The hammering process gives an asymmetrical shape despite
the general overall bowl shaped appearance. With hammer blows all over
the surface, the thickness of the metal varies over the entire bowl. The
homogeneity of the metal mixture is not ideal; some bowls even show
areas of pure copper which turn green from oxidation. Some bowls have
engraved inscriptions which distort the symmetry of the bell, changing
the sound.
Are imperfections undesirable? If not too dominating,
irregular pulsation contributes to the beneficial effects that singing
bowls have on people. Pulsating sound waves cause hypnotic and trance
states. Like listening to the waves of the ocean or to the heart beat of
our mother they make us feel good. They have a soothing and calming
effect. Studies have shown that vibrations from rhythmic sounds have a
profound effect on brain activity. Drumming, rhythmic singing, and
movement can transport a person into other realms of reality. Shamans
use these methods for healing, but it is not exclusively their realm,
people from all over the world use the same techniques to go into trance
states.
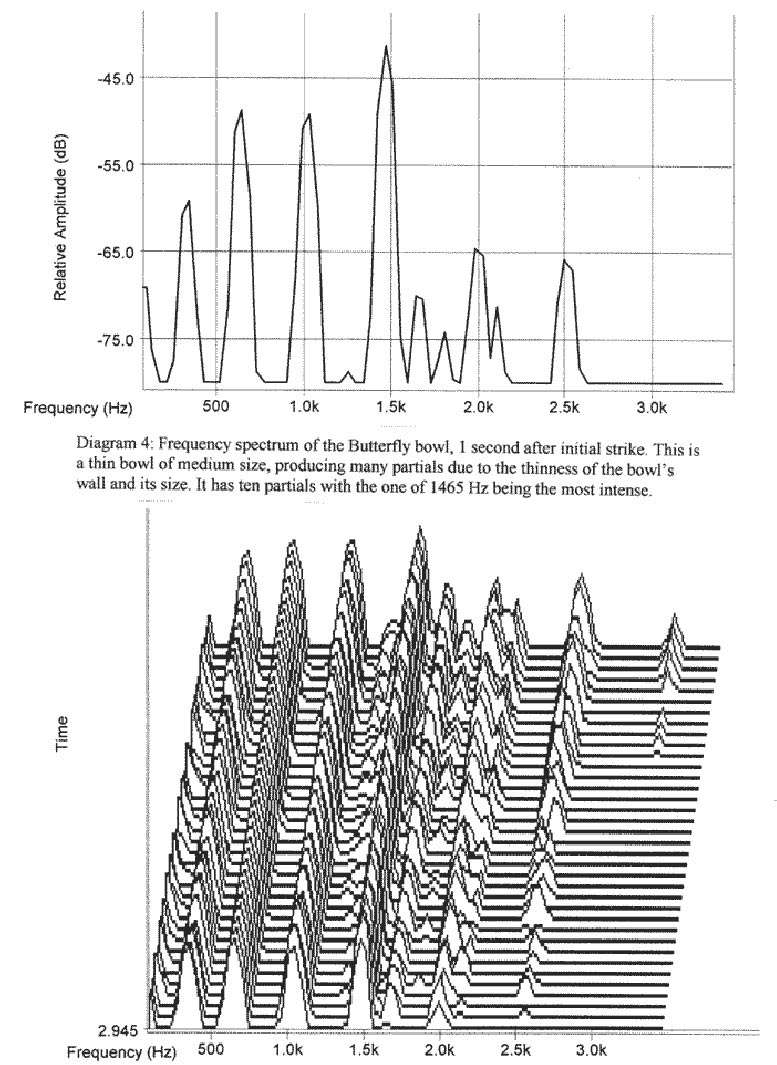
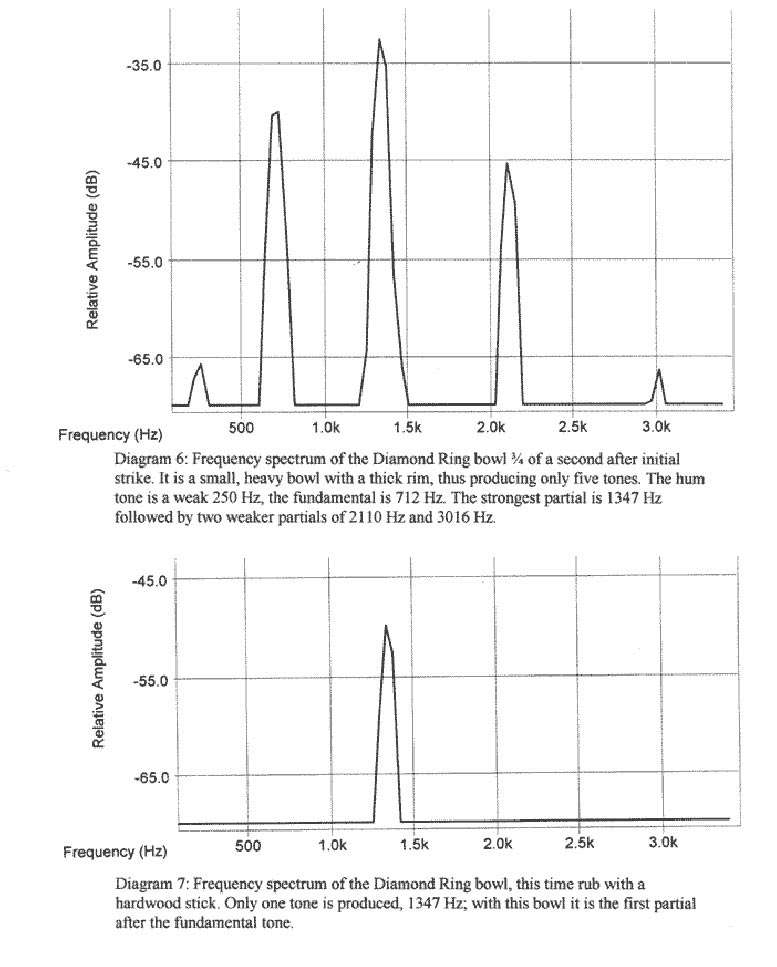
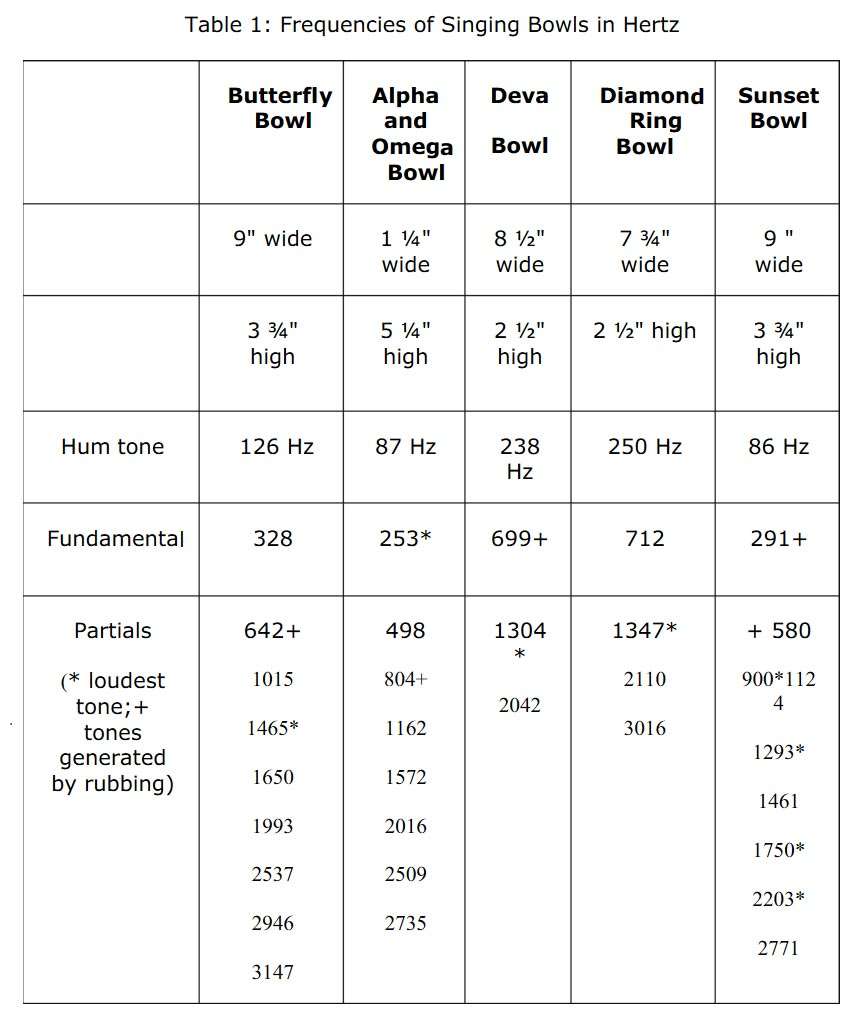
I have done a sound analysis of some of my singing bowls. The
computer generated diagrams show the patterns of sound waves when of all
the tones are sounding at the same time. Each position on the diagram
shows all the tones at that moment, each diagram shows a series of
moments in time. As each tone has a different frequency and amplitude,
tones will strengthen or cancel each other out as they go along. This
produces many different patterns, which show up when we scale up the
diagram. It is like a microscope, getting a bigger look at a smaller
moment of time. Each magnification reveals more detail and more
patterns. Each bowl is identified by a name I have given to it.
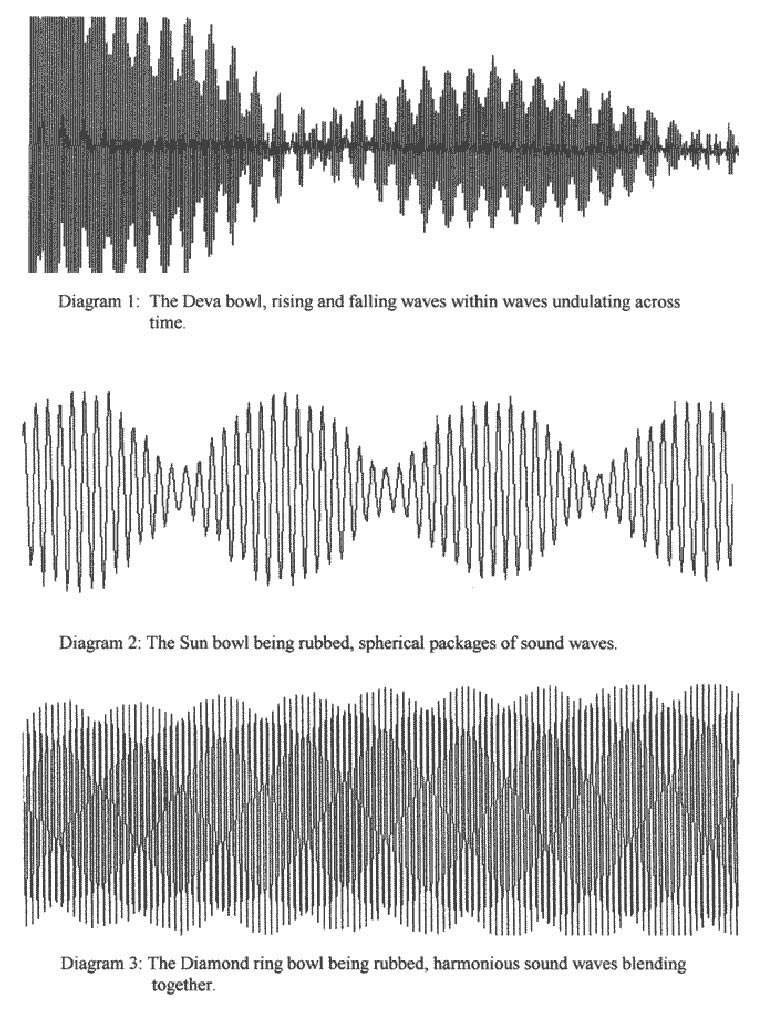
Diagram 1 is the wave patterns of the Deva bowl. The diagram length is
10 seconds. Groups of sound patterns rise and fall within other groups
of sound patterns. All are harmoniously structured in sine waves, rising
and falling as they travel across time.
Diagram 2 has a length of
0.81 seconds and shows a close-up of the sound patterns of the Sun bowl
while it is being rubbed with a hardwood stick to accentuate the
partials. Here the wave pattern is almost circular in form.
Diagram 3 shows the sound waves of the Diamond Ring bowl as it is rubbed
with a hardwood stick. This produces a fluent sound pattern. The diagram
length is 1.37 seconds.
|